Resistor cube is made of 12 resistors connected to form a cube. Finding equivalent resistance between two nodes of the cube, is one of the most complicated problems in physics. But when resistors in the cube are identical, you can take benefits of its symmetry and find equivalent resistance between each pair of its vertices (or nodes). When identical resistors are connected to form a cube, there are three different pairs of vertices: vertices on the space diagonal, vertices on the face diagonal, and vertices on one edge. In this article created in three parts, I will show you how you can find equivalent resistance between any pairs of vertices in a resistor cube made of equal resistors.
Equivalent resistance between two vertices on the space diagonal
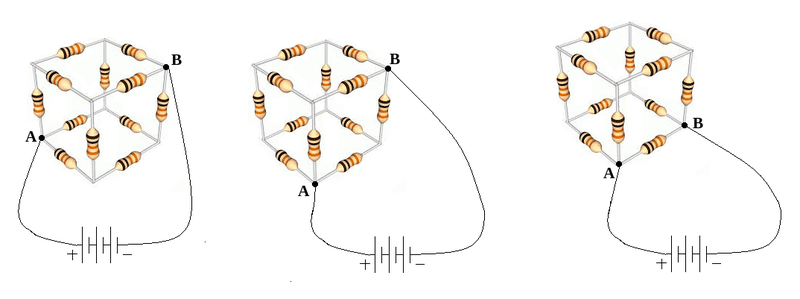
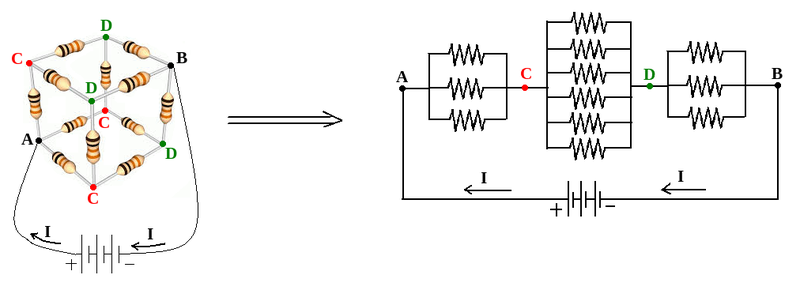
The picture on the left below shows resistor cube whose vertices on one of its space diagonals are connected to a voltage source. These two vertices are labelled by A, and B.
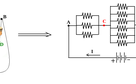
Edges labelled by AC are symmetric paths in front of electric current I, that enters A. So the current I, splits equally between these three branches, and electric potential drop on them are also the same. So electric potential on vertices labelled by C, are equal, and these vertices can be shorted. This argument is also applicable to the vertices labelled by D, and they can be shorted. The picture on the right below shows the electric circuit of our resistor cube, with shorted vertices C, and D.
If the resistance of each resistor is r, you can find equivalent resistance of parallel resistors as:
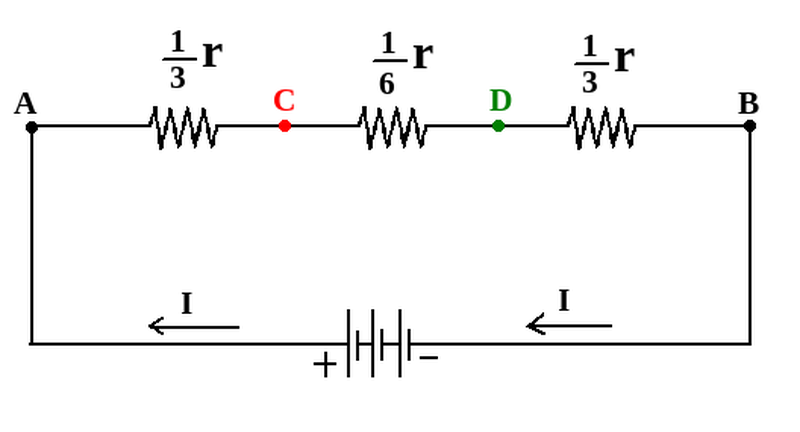
RAC = RDB = (1/3)r , and RCD = (1/6)r
So the above electric circuit, can be simplified as:
So the electric resistance between points A, and B, is:
RAB= RAC + RCD +RDB
So: RAB=(2/3)r + (1/6)r= (5/6)r
If: r=1 Ω then: RAB= 5/6 Ω
Equivalent resistance between two vertices on the face diagonal
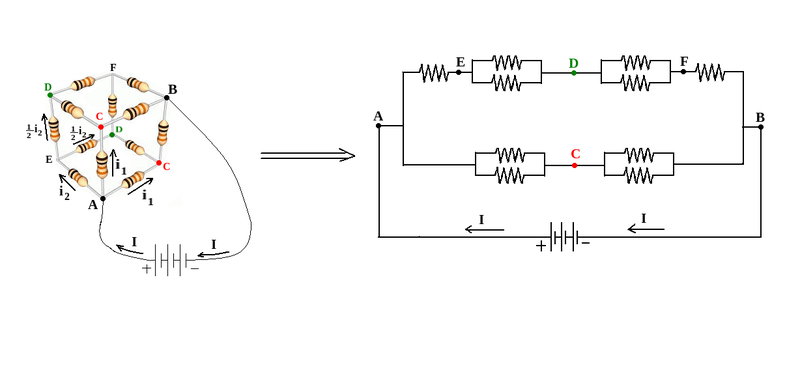
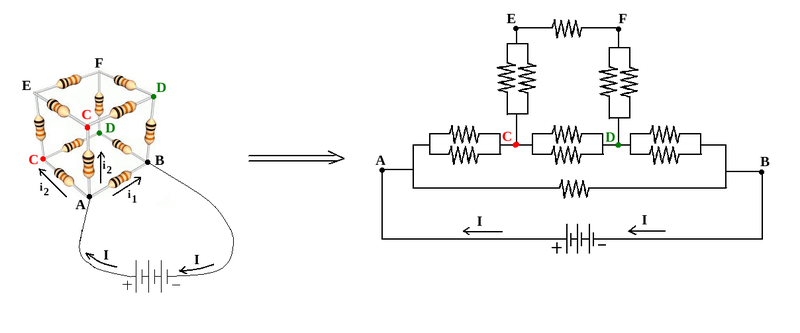
The picture on the left below shows resistor cube whose vertices on one of its face diagonals are connected to a voltage source. These two vertices are labelled by A, and B.
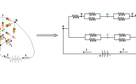
In front of electric current I, entering A, edges labelled by AC are symmetric paths , with equal electric currents represented by i1 ; but the edge labelled by AE differs from AC edges and electric current flowing on it, is: i2=I - 2i1 . So electric potential on vertices labelled by C, are the same, and these vertices can be shorted. This kind of argument is applicable to the vertices labelled by D, and they can be shorted.
Due to the symmetric distribution of currents, electric currents on edges AC and CB, are equal. So the electric current i1 , flowing on AC , enters in vertex C, and electric current i1 , flowing on CB, leaves vertex C. So there is not any electric current on edges labelled by CD. They behave as if there is not any connection between C and D.
The picture on the right below is the electric circuit of this cube with shorted vertices C and D, and without any connection between C and D.
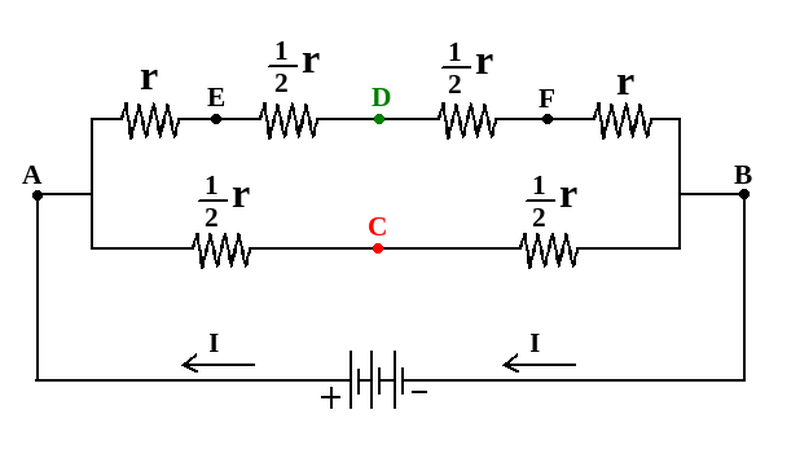
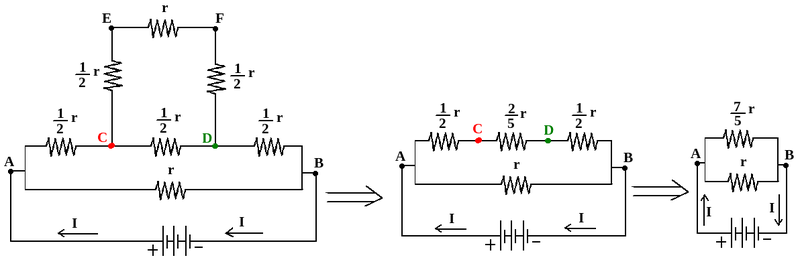
So the electric resistance between points A, and B, is:
So: RAB= (3/4)r
If: r=1 Ω then: RAB= 3/4 Ω
Equivalent resistance between two vertices on one edge
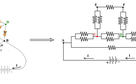
For this case too, there are three branches in front of electric current I, entering vertex A; two of them which are represented by AC, are symmetric. So electric potential at vertices labelled by C, are equal, and these vertices can be shorted. This is the case for the vertices labelled by D, and they can be shorted.
So the electric resistance between vertices A, and B, is:
So: RAB= (7/12)r
If: r=1 Ω then: RAB= 7/12 Ω

View All Comments /Add Comment